Reading Assignments
Math 104 Calculus II, Spring 2019
This page uses MathJax to display mathematical notation, so please let me know if any part isn't clear.
Be sure to check back, because there will certainly be some changes during the semester.
All numbers indicate sections from APEX Calculus, Version 4.0, and check the Errata for corrections to the text.
For Friday January 25 (Due 1/24 @ 8:00 pm)
Section 6.1 Substitution
Reading Questions
- Substitution attempts to undo one of the techniques of differentiation. Which one is it?
- Use u-substitution to find an antiderivative of \( f(x) = 5x^4 \sin(x^5) \)
- Explain why \( \dst \int 2x\cos(x^2) \sin(x^2)^2 dx\) and \( \dst\int \frac{(\ln(x)+1)^2}{x} dx \) are essentially the same integral after performing a substitution.
Submit answers through onCourse
For Monday January 28 (Due 1/27 @ 8:00 pm)
Section 2.7 Derivatives of Inverse Functions
Reading Questions
- Why do you think we are studying the inverse trig functions now?
- Find an antiderivative of \( f(x) = \dst \frac{x^2}{ 1 + x^6}\)
Submit answers through onCourse
For Wednesday January 30 (Due 1/29 @ 8:00 pm)
Section 6.2 Integration by Parts
Reading Questions
- Integration by parts attempts to undo one of the techniques of differentiation. Which one is it?
- Use integration by parts to find an antiderivative of \(f(x) = 2x e^{4x}\)
Submit answers through onCourse
For Friday February 1 (Due 1/31 @ 8:00 pm)
Section 6.2 Integration by Parts
Reading Questions Would you use u-substitution or integration by parts to find each anti-derivative? Find the antiderivative and explain why you chose the method you did.
- \( \int \cos(x) \sin(x) dx \)
- \( \int e^x x^2 dx \)
Submit answers through onCourse
For Monday February 4 (Due 2/3 @ 8:00 pm)
Section 5.5 Numerical Integration
Reading Questions
- Why would you ever want to numerically approximate an integral?
- Which would you expect to be MOST accurate: a Right Hand approximation, a Trapezoidal approximation, or a Simpson's approximation? Why?
- Which would you expect to be LEAST accurate: a Right Hand approximation, a Trapezoidal approximation, or a Simpson's approximation? Why?
Submit answers through onCourse
For Wednesday February 6 (Due 2/5 @ 8:00 pm)
Section 7.2 Volume by Cross-Sectional Area; Disk and Washer
Reading Questions
- Let R be the rectangle formed by the x-axis, the y-axis, and the lines y=1 and x=4. Describe the shape of the solid formed when R is rotated about the x-axis.
- Let T be the triangle formed by the lines y=2x, x=2 and the x-axis. Describe the shape of the solid formed when T is rotated about the line y = -1.
Submit answers through onCourse
For Friday February 8
Section 7.2 Volume by Cross-Sectional Area; Disk and Washer
Re-read the section, but no Reading Questions for today
For Monday February 11 (Due 2/10 @ 8:00 pm)
Section 7.4 Arc Length and Surface Area
Reading Questions
- Set up the integral that gives the length of the curve \( y=\sin(2x)\) from \(x=0\) to \( x=2\pi\).
- Set up the integral that gives the surface area of the surface formed when the curve \( y=x^2 + 2\) from \(x=0\) to \(x=3\) is rotated about the x-axis.
Submit answers through onCourse
For Wednesday February 13 (Due 2/12 @ 8:00 pm)
Section 6.8 Improper Integration
Reading Questions
- Explain why \( \dst\int_1^{\infty} \frac{1}{x^2} dx \) is improper.
- Explain why \( \dst\int_0^1 \frac{1}{x^2} dx \) is improper.
- Explain why \( \dst\int_{-1}^1 \frac{1}{x^2} dx \) is improper.
Submit answers through onCourse
For Friday Feburary 15 (Due 2/14 @ 8:00 pm)
Section 6.8 Improper Integration
Reading Questions
Suppose f and g are continuous and \( 0 < f(x) < g(x)\) for \( x > 0\).
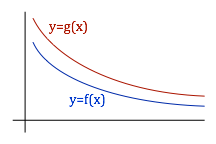
- If the improper integral \( \int_1^{\infty} g(x) dx \) converges, what can you conclude about the improper integral \( \int_1^{\infty} f(x) dx \)?
- If the improper integral \( \int_1^{\infty} f(x) dx \) diverges, what can you conclude about the improper integral \( \int_1^{\infty} g(x) dx \) ?
- If the improper integral \( \int_1^{\infty} f(x) dx \) converges, what can you conclude about the improper integral \( \int_1^{\infty} g(x) dx \) ?
Submit answers through onCourse
For Monday February 18
Q & A for Exam 1. No Reading Assignment for today.
For Wednesday February 20 (Due 2/19 @ 8:00 pm)
Section 8.1 Sequences
Reading Questions
- Does the following sequence converge or diverge? Be sure to explain your answer.
1, 3, 5, 7, 9, 11, 13, . . . - Find a symbolic expression for the general term ak of the sequence
1, 2, 4, 8, 16, 32, . . . - Is the following sequence bounded? Is it monotone? Explain. \[ 1, -\frac{1}{2}, \frac{1}{4}, -\frac{1}{8}, \frac{1}{16}, -\frac{1}{32}, \ldots \]
Submit answers through onCourse
For Friday February 22 (Due 2/21 @ 8:00 pm)
Section 8.2 Infinite Series
Reading Questions
- There are two sequences associated with every series. What are they?
- Does the geometric series \( \dst \sum \left( \frac{1}{4}\right)^k\) converge or diverge? Why?
- Does the geometric series \( \dst \sum \left( \frac{\pi}{e}\right)^k\) converge or diverge? Why?
Submit answers through onCourse
For Monday February 25 (Due 2/24 @ 8:00 pm)
Section 8.2 Infinite Series
Reading Questions
- What does the nth-Term Theorem tell you about the series \( \dst \sum 2^k \)?
- What does the nth-Term Theorem tell you about the series \( \dst \sum \frac{1}{k} \)?
Submit answers through onCourse
For Wednesday February 27 (Due 2/26 @ 8:00 pm)
Section 8.3 Integral and Comparison Tests
Reading Questions
- What does the Integral Test tell you about the series \( \dst \sum \frac{1}{k^3} \)?
- What does the Integral Test tell you about the series \( \dst \sum \frac{1}{\sqrt{k}} \)?
- What does the Direct Comparison Test tell you about the series \( \dst \sum \frac{1}{k^3 + \sqrt{k}} \)?
Submit answers through onCourse
For Friday March 1 (Due 2/28 @ 8:00 pm)
Section 8.3 Integral and Comparison Tests
Reading Questions
- Use the Limit Comparison Test to show that \( \dst\sum \frac{1}{n^2 - n}\) converges.
- Explain why it would have been more difficult to apply the Direct Comparison Test to this series.
Submit answers through onCourse
For Monday March 4 (Due 3/3 @ 8:00 pm)
Section 8.5 Alternating Series and Absolute Convergence
Reading Questions
Consider the series \( \sum_{k=1}^\infty (-1)^k \frac{1}{k^2}\)
- Why does this series converge?
- How closely does \( S_{50}\), the 50th partial sum, approximate the value of the series? Why?
Submit answers through onCourse
For Wednesday March 6
Section 8.5 Alternating Series and Absolute Convergence
Re-read the section, but no Reading Questions for today. Monday's snow day messed up the schedule a bit.
For Friday March 8
Section 8.5 Alternating Series and Absolute Convergence
Re-read the section, but no Reading Questions for today
March 11 - 15
Spring Break. Surprisingly, no Reading Assignments.
For Monday March 18 (Due 3/17 @ 8:00 pm)
Section 8.6 Power Series
Reading Questions
- How do power series differ from the series we have looked at up to this point?
- What is the interval of convergence of a power series? Explain in your own words.
Submit answers through onCourse
For Wednesday March 20 (Due 3/19 @ 8:00 pm)
Section 8.7 Taylor Polynomials
Section 8.8 Taylor Series
Reading Questions
- What is the difference between a Taylor polynomial and a Taylor series?
- What is the difference between a Taylor series and a Maclaurin series?
- Why would you ever want to compute a Taylor series for a function like sin(x)?
Submit answers through onCourse
For Friday March 22
Section 8.8 Taylor Series
Reread the section. No new Reading Questions for today.
For Monday March 25
Q & A for Exam 2. No Reading Assignment for today.
For Wednesday March 27 (Due 3/26 @ 8:00 pm)
Section 12.1 Introduction to Multivariable Functions
Reading Questions
- Describe the level curves of the function \(f(x,y)= x^2 - y\)
- Describe the level surfaces of the function \(g(x,y,z)=x^2+y^2+z^2\)
Submit answers through onCourse
For Friday March 29 (Due 3/28 @ 8:00 pm)
Section 12.3 Partial Derivatives
Reading Questions
- For a function \(f(x,y)\), what information does \( f_x(2,3)\) give?
- How many second-order partial derivatives does a function \(g(x,y)\) have? Why?
Submit answers through onCourse
For Monday April 1
Section 12.3 Partial Derivatives
Reread the section. No new Reading Questions for today.
For Wednesday April 3 (Due 4/2 @ 8:00 pm)
Section 10.2 An Introduction to Vectors
Section 10.3 The Dot Product
Reading Questions
- Give the unit vector in the same direction as \( \vec{\,v}=\langle 2,3 \rangle\)
- If the dot product \( \vec{\,u}\cdot \vec{\,v}=0\), what does this tell you about the vectors?
Submit answers through onCourse
For Friday April 5 (Due 4/4 @ 8:00 pm)
Section 11.2 Calculus and Vector-Valued Functions
Section 11.3 The Calculus of Motion
Reading Questions
Let \( \vec{\;r}(t) = \langle \sin(2t),t^2 \rangle \)
- Find \( \vec{\;r}\ ' (1)\)
- What is the velocity of \( \vec{\;r}(t)\) at time \( t=1\)?
- What is the speed of \( \vec{\;r}(t)\) at time \(t=1\)?
Submit answers through onCourse
For Monday April 8 (Due 4/7 @ 8:00 pm)
Section 12.6 Directional Derivatives
Reading Questions
- What does the directional derivative \( D_{\vec{\,u}} f(a,b)\) measure?
- If \(f(x,y) = 3xy^2 + 2x-4y^2\), what is \(\nabla f(x,y)\) ?
Submit answers through onCourse
For Wednesday April 10
Flex Day. No Reading Assignment due.
For Friday April 12
No Class today, so no Reading Assignment.
For Monday April 15 (Due 4/14 @ 8:00 pm)
Section 12.8 Extreme Values
Reading Questions
- Where can the local extrema of a function f(x,y) occur?
- Why does the term "saddle point" make sense?
For Wednesday April 17
Section 12.8 Extreme Values
Re-read the section, but no Reading Questions for today
For Friday April 19 (Due 4/18 @ 8:00 pm)
Section 13.1 Iterated Integrals and Area
Reading Questions
- Why would you want to calculate an iterated integral?
- Why would you want to switch the order of integration in an iterated integral?
Submit answers through onCourse
For Monday April 22 (Due 4/21 @ 8:00 pm)
Section 13.2 Double Integration and Volume
Reading Questions
- If \(f(x,y)\) is a function of two variables and \(R\) is a rectangle in the xy-plane, what does \( \int\int_R f(x,y)\, dA\) measure?
- Explain the idea of Fubini's Theorem in a couple of sentences in your own words.
Submit answers through onCourse
For Wednesday April 24
Section 13.2 Double Integration and Volume
Re-read the section, but no Reading Questions for today
For Friday April 26 (Due 4/25 @ 8:00 pm)
Section 13.2 Double Integration and Volume
Re-read the section, but no Reading Questions for today
For Monday April 29
Q & A for Exam 3. No Reading Assignment for today.
For Wednesday May 1
Section 13.4 Center of Mass
Reading Questions
- Tell a brief story where you would want to find the center of mass of a lamina with variable density.
- Take a look at Theorem 13.4.3. Is there anything surprising, or confusing, in the statement of the theorem?
Submit answers through onCourse
For Friday May 3
The BIG Picture for the semester. No Reading Assignment for today.
