|
Be sure to check back, because this may change during the semester.
All numbers indicate sections from
Linear Algebra and Its Applications, 4th Edition by Lay
For Thursday September 3
Section 1.1 Systems of Linear Equations
Section 1.2 Row Reduction and Echelon Forms
Section 1.3 Vector Equations
To read:
All
Reading Questions
Let 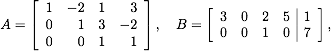 u=(1,2,-1) and v=(-3,1,5). u=(1,2,-1) and v=(-3,1,5).
- Is A in reduced echelon form? Why or why not?
- What are the pivot columns of A? What are the values of the pivots of A?
- If B is the augmented matrix of a linear system, does the system have any free variables? If so, what are they?
- Write the vector w=(-3, 8, 7) as a linear
combination of u and v.
Submit answers through onCourse
For Tuesday September 8
Section 1.4 The Matrix Equation Ax=b
Section 1.5 Solution Sets of Linear Systems
To read:
All
Reading Questions
- Let
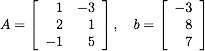
a. Does Ax = b have a solution for this specific value of b? Why or why not?
b. Does Ax = b have a solution for every b ∈ ℝ3? Why or why not?
- Explain the difference between a homogeneous system of equations and a non-homogeneous system of equations.
- If the system Ax = b is consistent and Ax = 0 has a
non-trivial solution, how many solutions does Ax =b have?
Submit answers through onCourse
For Thursday September 10
Section 1.7 Linear Independence
To read:
All
Reading Questions
Let 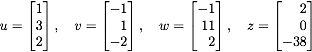
- Is the set of vectors {u, v} linearly independent or linearly dependent?
Explain.
- Is the set of vectors {u, v, w} linearly independent or linearly dependent? Explain.
- If the vectors u, v, w, and z form the columns of the matrix A, does Ax = 0 have a non-trivial solution? Explain.
Submit answers through onCourse
For Tuesday September 15
Section 1.8 Introduction to Linear Transformations
To read:
All
Reading Questions
- Suppose T: ℝ4 → ℝ5 is a linear transformation and T(x) = Ax
for some matrix A. What are the dimensions of A? Why?
- Give an example of a function T: ℝ2 → ℝ2
that is not a linear transformation. Explain.
Submit answers through onCourse
For Thursday September 17
Section 1.9 The Matrix of a Linear Transformation
To read:
All
Reading Questions
- Give the matrix A for the linear transformation
T:ℝ2 → ℝ2 that expands vertically by a factor of 4.
- Let T:ℝ5 → ℝ3 be a linear transformation with
standard matrix A where A has three pivots. Is T one-one? Explain.
- Let T:ℝ3 → ℝ5 be a linear transformation with
standard matrix A where A has three pivots. Is T one-one? Explain.
Submit answers through onCourse
For Tuesday September 22
Section 2.1 Matrix Operations
Section 2.2 Inverse of a Matrix
To read:
All
Reading Questions
- Give one way in which matrix multiplication differs from multiplication of real numbers.
- Let
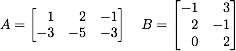
Compute the following products or explain why it is impossible:
AB, BA, BAT
- Let
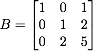 . Find B-1.
. Find B-1.
- Give an example of a 2 x 2 singular matrix.
- If A is invertible, how many solutions does Ax=b have? Why?
Submit answers through onCourse
For Thursday September 24
Section 2.3 Characterizations of Invertible Matrices
To read:
All
Reading Questions
- If A is an n x n matrix with n pivots, how many solutions does Ax=b have? Why?
- If A is an invertible matrix, are the rows of A a linearly independent set or a linearly dependent set? Why?
You should think about these, but no need to send in your answers through onCourse.
For Tuesday September 29
Exam 1 tonight No Reading Assignment.
For Thursday October 1
Section 3.1 Introduction to Determinants
Section 3.2 Properties of Determinants
To read:
All
Reading Questions
- Let
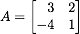 .
Find det(A). .
Find det(A).
- Let
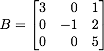 .
Find det(B). .
Find det(B).
- Why do we care about finding the determinant of a matrix?
Submit answers through onCourse
For Tuesday October 6
Section 4.1 Vector Spaces and Subspaces
Section 4.2 Null Spaces, Column Spaces, and Linear Transformations
To read:
All
Reading Questions
- Give an example of a subset of ℝ2 that is not a subspace
of ℝ2.
- Let ℙ4 denote the set of all polynomials of degree 4 or less with real coefficients. Give examples of two vectors in the vector space ℙ4.
- If the columns of A are linearly independent, what is Nul(A)? Why?
- If A is 6 x 9 with 6 pivots, what is Col(A)? Why?
Submit answers through onCourse
For Thursday October 8
No class today. I'll be at a conference.
For Tuesday October 13
Fall Break. No Reading Assignment.
For Thursday October 15
Section 4.3 Linearly Independent Sets; Bases
To read:
All
Reading Questions
Let 
- Do the columns of A form a basis for ℝ3? Explain.
- Give a basis for Col(A).
- Give a basis for Nul(A).
Submit answers through onCourse
For Tuesday October 20
Re-read the section, but no Reading Questions for today.
For Thursday October 22
Section 4.4 Coordinate Systems
Section 4.5 The Dimension of a Vector Space
To read:
All
Reading Questions
Let 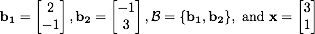
- Show that B is a basis for ℝ2.
- Find the coordinate vector [x]B of x relative to B.
- What is the dimension of ℝ3? Why? Does this make sense geometrically?
Submit answers through onCourse
For Tuesday October 27
Exam 2 tonight. No Reading Assignment.
For Thursday October 29
Section 4.9 Applications to Markov Chains
To read:
All
Reading Questions
- What is the point of studying Markov chains?
- What is a steady state vector for a stochastic matrix P?
- What is special about regular stochastic matrices?
Submit answers through onCourse
For Tuesday November 3
Section 5.1 Eigenvectors and Eigenvalues
Section 5.2 The Characteristic Equation
To read:
All, but you can skim the part of Section 5.2 labeled Determinants. One path through the text is to skip Chapter 3, so that is why this information is included here.
Reading Questions
- Let A =
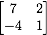 .
Verify that x = .
Verify that x = 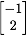 is an eigevector of A with corresponding eigenvalue λ = 3.
is an eigevector of A with corresponding eigenvalue λ = 3.
- Suppose A is 3x3 with eigenvalues 1, 2, and 5. What is the dimension of nul(A)?
- Let A be the matrix from #1. Find the characteristic equation of A.
Submit answers through onCourse
For Thursday November 5
Section 5.3 Diagonalization
To read:
All
Reading Questions
- What is the point of finding a diagonalization of a matrix?
- If A is 4 x 4 with eigenvalues 1, 2, 0, 3, is A diagonalizable? Explain.
Submit answers through onCourse
For Tuesday November 10
Section 5.6 Discrete Dynamical Systems
To read:
All
Reading Questions
Consider the discrete dynamical system described by xk+1 = A xk where A is a 2 x 2 matrix.
- If the origin is an attractor, what do you know about the eigenvalues of A? Why?
- If the origin is a saddle, what do you know about the eigenvalues of A? Why?
Submit answers through onCourse
For Thursday November 12
Section 6.1 Inner Product, Length, and Orthogonality
To read:
All
Reading Questions
- Are the vectors
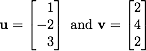 orthogonal in ℝ3? Explain.
orthogonal in ℝ3? Explain.
- Give a geometric interpretation of your answer to 1.
- Let H be the yz-plane in ℝ3. What is the orthogonal complement of H?
Submit answers through onCourse
For Tuesday November 17
Section 6.2 Orthogonal Sets
To read:
All
Reading Questions
- Let H be the yz-plane in ℝ3. Give an orthogonal basis for H.
- Let w be the orthogonal projection of y onto u. In what direction does w point? In what direction does y - w point?
Submit answers through onCourse
For Thursday November 19
Section 6.3 Orthogonal Projections
To read:
All
Reading Questions
Let 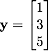 in ℝ3 and let W be the xy-plane in ℝ3.
in ℝ3 and let W be the xy-plane in ℝ3.
- Find the orthogonal projection of y onto W.
- Is there a point in W that is closer to y than your answer in 1? Explain.
Submit answers through onCourse
For Tuesday November 24
Exam 3. No Reading Assignment
For Thursday November 26
Thanksgiving Break. No Reading Assignment.
For Tuesday December 1
Section 6.4 The Gram-Schmidt Process
To read:
Read the section, but no Reading Questions for today.
For Thursday December 3
Section 6.5 Least-Squares Problems
To read:
All
Reading Questions
- In your own words, what is the point of this section?
- Does every system Ax=b have a least squares solution? Explain.
- If a system Ax=b has a least squares solution, must it be unique? Explain.
Submit answers through onCourse
For Tuesday December 8
Section 10.1 Introduction and Examples
Section 10.2 The Steady-State Vector and Google's PageRank
Read the sections, but no Reading Questions for today.
For Thursday December 10
Reread Section 10.1 and 10.2, but no Reading Questions for today.
|