Reading Assignments - Math 104 Calculus II - Spring 2014

Be sure to check back, because this may change during the semester.

All numbers indicate sections from Calculus by Taalman and Kohn.

For Friday January 24

Section 5.1 Integration by Substitution

To read

• Topics:
  • The Art of Integration
  • Undoing the Chain Rule
  • Choosing a Useful Substitution
  • Finding Definite Integrals by Using Substitution
• Examples: 1 - 6

Reading Questions

1. Substitution attempts to undo one of the techniques of differentiation. Which one is it?
2. Use u-substitution to find an antiderivative of f(x) = 3x² cos(x³)
3. Explain why ∫ cos(x) sin(x)² dx and ∫ ln(x)² / x dx are essentially the same integral after performing a substitution.

Submit answers through onCourse

For Monday January 27

Section 2.6 Inverse Trigonometric Functions

To read

• Topics:
  • Derivatives of Inverse Trigonometric Functions
• Example: 3

Reading Questions

1. Why do you think we are studying the inverse trig functions now?
2. Find an antiderivative of f(x) = x² / ( 1 + x⁶ )

Submit answers through onCourse

For Wednesday January 29

Section 5.2 Integration by Parts

To read

• Topics:
  • Undoing the Product Rule
  • Strategies for Applying Integration by Parts
  • Finding Definite Integrals by Using Integration by Parts
• Examples: 1 - 4

Reading Questions

1. Integration by parts attempts to undo one of the techniques of differentiation. Which one is it?
2. Use integration by parts to find an antiderivative of f(x) = 2x e^4x

Submit answers through onCourse

For Friday January 31

Section 5.2 Integration by Parts

To read

• Re-read the section

Reading Questions
Would you use u-substitution or integration by parts to find each anti-derivative? Find the antiderivative and explain why the other method would not work.

1. ∫ cos(x) sin(x) dx
2. ∫ e^x cos(x) dx

Submit answers through onCourse

For Monday February 3

Section 5.6 Improper Integrals

To read

• Topics:
  • Integrating over an Unbounded Interval
  • Integrating Unbounded Functions
  • Improper Integrals of Power Functions
• Examples: 1, 2, 3

Reading Questions

1. Explain why ∫₁^∞ 1/x² dx is improper.
2. Explain why ∫₀¹ 1/x² dx is improper.
3. Explain why ∫_-1¹ 1/x² dx is improper.

Submit answers through onCourse

For Wednesday February 5

Section 5.6 Improper Integrals

To read

• Topics:
  • Determining Convergence or Divergence with Comparisons
• Examples: 4

Reading Questions
Suppose f and g are continuous and 0 ≤ f(x) ≤ g(x) for x>0.

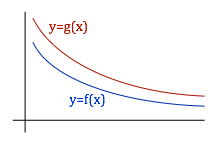
1. If the improper integral ∫₁^∞ g(x) dx converges, what can you conclude about the improper integral ∫₁^∞ f(x) dx ?
2. If the improper integral ∫₁^∞ f(x) dx diverges, what can you conclude about the improper integral ∫₁^∞ g(x) dx ?
3. If the improper integral ∫₁^∞ f(x) dx converges, what can you conclude about the improper integral ∫₁^∞ g(x) dx ?

Submit answers through onCourse

For Friday February 7

Section 5.7 Numeric Integration

To read

• Topics:
  • Approximations and Error
  • Error in Left and Right Sums
• Example: 1

Reading Questions

1. Why would we want to approximate a definite integral?
2. When approximating an integral, which would you expect to be more accurate, LEFT(5) or LEFT(20)? Why?
3. If a function f(x) is decreasing on an interval, will LEFT(n) underestimate or overestimate the integral? Why?

Submit answers through onCourse

For Monday February 10

Section 5.7 Numeric Integration

To read

• Topics:
  • Error in Trapezoid and Midpoint Sums
• Example: 2

Reading Questions

1. If a function f(x) is concave down on an interval, will TRAP(n) overestimate or underestimate the integral?
2. Consider the integral ∫_-2¹ x³ dx. Is 4 a valid value for M in Theorem 5.27? Why or why not?

Submit answers through onCourse

For Wednesday February 12

Section 6.1 Volumes by Slicing

To read

• Topics:
  • Approximating Volume by Slicing
  • Volume as a Definite Integral of Cross-Sectional Area
  • Volumes by Disks and Washers
• Examples: 1, 2, 3
• Another optional resource are the videos at Kahn Academy on Solids of Revolution. The first two, "Disk method around x-axis" and "Generalizing disc method around x-axis", are relevant for today.

Reading Questions

1. Let R be the rectangle formed by the x-axis, the y-axis, and the lines y=1 and x=3. Describe the shape of the solid formed when R is rotated about the x-axis.
2. Let T be the triangle formed by the lines y=2x, x=3 and the x-axis. Describe the shape of the solid formed when T is rotated about the x-axis.

Submit answers through onCourse

For Friday February 14

Section 6.1 Volumes by Slicing

To read

• Re-read the topics from Wednesday
• Example: 5

Reading Questions

1. Let R be the rectangle formed by the x-axis, the y-axis, and the lines y=1 and x=3. Describe the shape of the solid formed when R is rotated about the line y=-5.
2. Let T be the triangle formed by the lines y=2x, y=6 and the y-axis. Describe the shape of the solid formed when T is rotated about the x-axis.

Submit answers through onCourse

For Monday February 17

Section 3.6 l'Hopital's Rule

To read

• Topics:
  • Geometrical Motivation for l'Hopital's Rule
  • l'Hopital's Rule for the Indeterminate Forms 0/0 and ∞/∞
  • Using Logarithms for the Indeterminate Forms 0⁰, 1^∞, and ∞⁰
• Examples: 1, 2, 3

Reading Questions

1. Does l'Hopital's Rule apply to lim_{(x -> ∞)} x² / e^x ? Why or why not?
2. Does l'Hopital's Rule apply to lim_{(x -> ∞)} x² / sin(x) ? Why or why not?
3. For each limit in #1 and #2 where l'Hopital's applies, use it to find the limit.

Submit answers through onCourse

For Wednesday February 19

Work on Project 1

To read

• A Guide to Writing in Mathematics Classes
• The Checklist for grading

For Friday February 21

Section 7.1 Sequences
Section 7.2 Limits of Sequences

To read

• Topics in 7.1:
  • Sequences of Numbers
  • Recursively Defined Sequences
  • Geometric and Arithmetic Sequences
  • Monotonic Sequences
  • Bounded Sequences
• Examples in 7.1: 1, 2, 3, 5, 7
  
  
• Topics in 7.2:
  • Convergence or Divergence of a Sequence
  • Theorems About Convergent Sequences
  • Convergence and Divergence of Basic Sequences
  • Bounded Monotonic Sequences
• Examples in 7.2: 1, 2, 3

Reading Questions

1. Does the following sequence converge or diverge? Be sure to explain your answer.
   1, 3, 5, 7, 9, 11, 13, . . .
2. Find a symbolic expression for the general term a_k of the sequence 1, 2, 4, 8, 16, 32, . . .
3. Is the following sequence bounded? Is it monotone? Why? 1, -1/2, 1/4, -1/8, 1/16, -1/32, . . .

Submit answers through onCourse

For Monday February 24

Section 7.3 Series

To read

• Topics:
  • Adding Up Sequences to Get Series
  • Convergence and Divergence of Series
  • The Algebra of Series
  • Geometric Series
• Examples: 1, 3, 4

Reading Questions

1. There are two sequences associated with every series. What are they?
2. Does the geometric series Σ (1/4)^k converge or diverge? Why?
3. Does the geometric series Σ (π/e)^k converge or diverge? Why?

Submit answers through onCourse

For Wednesday February 26

For Friday February 28

Section 7.4 Introduction to Convergence Tests

To read

• Topics:
  • An Overview of Convergence Tests for Series
  • The Divergence Test
  • The Integral Test
  • Convergence and Divergence of p-Series and the Harmonic Series
  • Approximating a Convergent Series
• Examples: 1, 2, 3

Reading Questions

1. What does the Divergence Theorem tell you about the series Σ 2^k ?
2. What does the Divergence Theorem tell you about the series Σ 1/k ?
3. What does the Integral Test tell you about the series Σ 1/k² ?
4. What does the Integral Test tell you about the series Σ 1/k ?

Submit answers through onCourse

For Monday March 3

Section 7.7 Alternating Series

To read

• Topics:
  • Alternating Series
  • Absolute and Conditional Convergence
  • The Curious Behavior of a Conditionally Convergent Series
• Examples: 1, 2

Reading Questions
Consider the series Σ (-1)^(k+1) /k^2

1. Why does this series converge?
2. How closely does S₅₀ approximate the value of the series? Why?

Submit answers through onCourse

For Wednesday March 5

Re-read Section 7.7 Alternating Series
No Reading Questions for today.

For Friday March 7

March 10 - 14

For Monday March 17

Section 8.1 Power Series

To read

• Topics:
  • Power Series
  • The Interval of Convergence of a Power Series
  • Power Series in x - x₀
• Examples: We'll go over a few different ones in class

Reading Questions

1. How do power series differ from the series we have looked at up to this point?
2. What is the interval of convergence of a power series? Explain in your own words.

Submit answers through onCourse

For Wednesday March 19

Section 8.2 Maclaurin Series and Taylor Series

To read

• Topics:
  • Maclaurin Polynomials and Taylor Polynomials
  • Taylor Series and Maclaurin Series
• Examples: 1, 2, 3

Reading Questions

1. What is the basic idea of constructing the n-th degree Taylor polynomial for a function f(x)? Do not give the formula, but explain in your own words in a few sentences.
2. What is the difference between a Taylor series and a Maclaurin series?

Submit answers through onCourse

For Friday March 21

Section 8.2 Maclaurin Series and Taylor Series

To read:

• Re-read the section for today.

Reading Questions

1. Use the Maclaurin series for f(x)=cos(x) to find the Maclaurin series for g(x)=cos(x²).
2. Use your answer to give the Maclaurin series for an antiderivative of cos(x²).

Submit answers through onCourse

For Monday March 24

Section 10.1 Cartesian Coordinates

To read

• Topics:
  • Three-Dimensional Space in Rectangular Coordinates
  • An Introduction to Planes
  • Distances, Spheres, and Cylinders
  • Quadric Surfaces
• Examples: 1, 2

Reading Questions
Consider the surface z = x² + y²

1. What does the trace in the xz-plane look like?
2. What does the section in the z=1 plane look like?
3. What does the section in the z=9 plane look like?

Submit answers through onCourse

For Wednesday March 26

Section 12.1 Functions of Two and Three Variables

To read

• Topics:
  • Functions of Two Variables
  • Graphing a Function of Two Variables
  • Functions of Three Variables
  • Level Curves and Level Surfaces
• Examples: 1, 3, 4

Reading Questions

1. Is the graph of the hyperboloid of one sheet x² + y² - z² = 1 the graph of a function of two variables? Explain.
2. Is the graph of the elliptic paraboloid z = x² + y² the graph of a function of two variables? Explain.

Submit answers through onCourse

For Friday March 28

Section 12.3 Partial Derivatives

To read

• Topics:
  • Partial Derivatives of Functions of Two and Three Variables
  • Higher Order Partial Derivatives
  • Finding a Function When the Partial Derivatives Are Given
• Examples: 1, 2, 4, 5

Reading Questions

1. For f(x,y), what information does f_x(1,0) give?
2. How many second-order partial derivatives does g(x,y,z) have? Why?

Submit answers through onCourse

For Monday March 31

Section 12.6 Extreme Values

To read

• Topics:
  • You'll need to understand Definition 12.35 The Gradient on pg 957
  • The Gradient at a Local Extremum
• Examples: 1 and 3. We'll talk about classifying extrema by methods other than the Second-Derivative Test.

Reading Questions

1. If f(x,y)= x²y + 3 x y, give an expression for ∇ f(x,y).
2. If the partials f_x and f_y exist everywhere, at what points (x₀, y₀) can f(x,y) have a local max or a local min?

Submit answers through onCourse

For Wednesday April 2

For Friday April 4

For Monday April 7

For Wednesday April 9

For Friday April 11

Section 13.1 Double Integrals over Rectangular

To read

• Topics:
  • Volumes
  • Double and Triple Summations
  • Iterated Integrals and Fubini's Theorem (pay special attention here)
• Examples: 1 and 2

Reading Questions

1. If f(x,y) is a function of two variables, what does ∫ ∫_R f(x,y) dA measure?
2. Explain the idea of Fubini's Theorem in a couple of sentences in your own words.

Submit answers through onCourse

For Monday April 14

For Wednesday April 16

Section 13.2 Double Integrals over General Regions

To read

• Topics:
  • General Regions in the Plane
  • Double Integrals over General Regions
  • Algebraic Properties of Double Integrals
• Examples: 1, 2, 3

Reading Questions
Let Ω be the region in the xy-plane bounded by the parabola y=x² and the horizontal line y=9.

1. Give values for a, b, g1(x), and g2(x) so that ∫ ∫_Ω f(x,y) dA = ∫_a^b ∫_g1(x)^g2(x) f(x,y) dy dx.
   
   
2. Give values for c, d, h1(y), and h2(y) so that ∫ ∫_Ω f(x,y) dA = ∫_c^d ∫_h1(y)^h2(y) f(x,y) dx dy.

Submit answers through onCourse

For Friday April 18

For Monday April 21

Section 9.2 Polar Coordinates

To read

• Topics:
  • Plotting Points in Polar Coordinates
  • Converting Between Polar and Rectangular Coordinates
  • The Graphs of Some Simple Polar Coordinate Equations
• Examples: 1, 2, 3, 4

Reading Questions

1. What do the coordinates (r, θ) in polar coordinates measure?
2. Why do you think we are studying polar coordinates now?
3. Is the graph of the polar function r = 4 cos(θ) is the graph of a function y=f(x)? Explain.

Submit answers through onCourse

For Wednesday April 23

For Friday April 25

Section 9.3 Graphing Polar Equations

To read

• Topics:
  • Using the θr - plane to Get Information About a Polar Graph
  • Symmetry in Polar Graphs
• Examples: 1 - 6

Reading Questions
Describe the shape of the graph of the following polar equations.

1. r = 2θ, θ≥ 0
2. r = 2 sin(θ)
3. r = sin(2θ)
4. r = sin(3θ)

Submit answers through onCourse

For Monday April 28

Section 13.3 Double Integrals Using Polar Coordinates

To read

• Topics:
  • Polar Coordinates and Double Integrals
  • Double Integrals in Polar Coordinates over General Regions
• Examples: 1, 4, 5

Reading Questions

1. Describe the shape of a polar "rectangle."
2. Why would you ever want to use polar coordinates to evaluate a double integral?

Submit answers through onCourse

For Wednesday April 30

For Friday May 2