Math 236 - Multivariable Calculus - Spring 2009

Selected Answers to Reading Assignments

For Friday January 23

1. Is (a.b).c the same as a.(b.c)?
   
   No, since the result of the dot product is a scalar, even if you considered scalar (a.b) dot c to mean scalar multiply (a.b) times c, it would not necessarily be equivalent to the scalar (b.c) times the vector a. If a and c were in different directions the two results would automatically be different.
   
   - Becky Johnson
   
   
2. In what direction does proj_ba point?
   
   Proj_ba points in the direction of b when 0<angle<(pi/2) and opposite b when (pi/2)<angle<pi
   
   - Jen Shields
   
   
3. When is comp_ba equal to comp_ab?
   
   Comp_ba is equal to compab when a and b are perpendicular to each other. This way the cos(π/2)=0 so the component is also zero in both cases.
   
   - Megan Geen
   
   Comp_ba is equal to the product of a and b divided by the magnitude of b, while comp_ab is equal to the product of a and b divided by the magnitude of a.
   Therefore, because the numerators of both comp_ba and comp_ab are the same, the denominators must be equal for the components to be equal. Comp_ba is equal to comp_ab when the magnitude of vector a is equal to the magnitude of vector b.
   
   - Aidan Kestigan
   

For Monday January 26

1. How is axb related to a and b geometrically?
   
   axb is orthogonal to both vector a and vector b. When the dot product of axb and the vector a (or b) is computed it will be zero. This is the definition of orthogonal vectors, that their dot product equals zero.
   
   - Alison Mehlhorn
   
   
2. Why don't we define axb for vectors in the plane?
   
   The cross product is defined only for vectors in V3. There is no corresponding operation for vectors in V2. As we know, axb is orthogonal to both a and b. If we define axb for vectors in the plane. There is no vector both orgonoal to both a and b in the plane at the same time. So we don't define axb for vectors in the plane.
   
   - Alfred Zhou
   

For Wednesday January 28

1. What information about a line L do you need to determine an equation for the line?
   
   The equation of a line can be found if you are given a vector parallel to the line and a point through which the line passes. You can also find the equation of a line if you are given 2 points (that lie on the line).
   
   - Kevin Hewitt
   
   
2. What information about a plane P do you need to determine an equation for the plane?
   
   You need a vector that is perpendicular to every vector lying in the plane and a point within the plane.
   
   - Rebecca Tate
   

For Friday January 30

1. Consider the graph of the vector-valued function r(t)=cos(t)i - sin(t)j. Is this the graph of a function y=f(x)? Explain.
   
   r(t)= cos(t)i- sin(t)j says x² + y² = 1 which is not a function y= f(x), because for any value of x in the domain except for plus or minus 1, there are two solutions.
   
   ex. If x=0, (as when t=pi/2), then plus or minus 1 are both solutions for y.
   
   Thus y does not equal f(x)
   
   - Luke Levy-Moore
   
   
2. What are some advantages to using vector-valued functions?
   
   It allows us to more easily find functions to model obscure things thats would be hard to model like the flight of the plane in the book.
   
   - Jon Lecznar
   
   

For Monday February 2

1. If r(t) is a vector-valued function, what geometric information does r'(t) give you?
   
   If r(t) is a vector valued function, r'(t) plots the tangent vector to the curve at the point t=a.
   
   - Julia Simundza
   
   
   
2. If the graphs of r(t) and s(t) are the same, will r'(0) be the same as s'(0)? Explain.
   
   r'(0) may not necessarily be the same as s'(0) even though r(t) and s(t) might have the same graphs because t is time and direction at time t may be different depending on the functions.
   
   - Eunice Bang
   

For Wednesday February 4

1. What quantity does the magnitude of the velocity vector give?
   
   Simply put: the quantity of the magnitude of the velocity vector gives the speed of the object as it moves along the curve (aka the instantaneous rate of change of arc length with respect to time)
   
   - Jeff Kleinschmidt
   
   
2. How would including air resistance in Example 3.4 complicate issues?
   Including air resistance would cause there to be another force in addition to gravity acting on the missile. The air resistance would cause the missile to slow down and fall back to the earth more quickly (at an earlier t). There would be a force vector F acting in the opposite direction of the path of the projectile. This new force vector would have to be added to the gravity vector.
   
   - Molly Thunberg
   

For Friday February 6

1. Explain the idea of curvature in your own words.
   
   The idea of curvature is to measure how sharp a curve is and by using arc length it is to calculate the curvature. Curvature is how much a curve curves, for example whether it is a sharp curve or a gentle curve. And by using vector-valued functions to trace the curve out with.
   
   - Staley Salazar
   
   
2. If the helix in Example 4.5 were changed to r(t)=< 2sin(t), 2cos(t), 4t²>, will the curvature still be constant? Don't actually do the calculation, but give an intuitive justification.
   
   No, the curvature would not be constant. The vector valued function as shown in 4.5 had a constant increase in height, or z. When you change 4t to 4t^2, that makes the height grow exponentially. The helix will still make a circle as it would before, but now the circles will be completed over increasing increments of height. This means that the curve distance is no longer constant for any section of the helix.
   
   - Kevin Hewitt
   

For Wednesday February 11

1. Suppose you are skiing down a hill that curves left. Describe the directions of the unit tangent, principle unit normal, and binormal vectors.
   
   The unit tangent vector points in the direction of the curve, and is instantaneously perpendicular to every point on the curve as it curves to the left. At the point where the hill curves, the unit tangent vector will point straight, in the direction that was being travelled before the trail curved.
   
   The principal unit normal vector, on the other hand, is orthogonal to the unit tangent vector and points toward the left, into the concave portion of the curve, in the same plane as the unit tangent vector.
   
   The binormal vector is orthogonal to both the unit tangent vector and the principal normal vector, and would therefore point up, off of the hill.
   
   - Vanessa D'Amico
   
   
2. Why do you want the normal component of acceleration to be small when steering a car through a curve?
   
   If the normal component of acceleration is too large, it may exceed the normal component of the force of friction between the tires and the highway, causing the car to skid off the road.
   
   - Mark Williamson
   

For Monday February 16

1. What does the trace in the xy-plane look like?
   
   The trace in the xy-plane looks like the parabola y=x^2 because in the xy-plane we set z=0 in the equation y=x^2+z^2.
   
   -Stephanie Jones
   
   
2. What do the traces in the planes y=k look like?
   
   The traces on the plane y=k look like the circle x^2+z^2=k, where for larger values of k (or y), we get a larger radius, resulting in larger circles.
   
   - Laura Richardson
   
   

For Friday February 20

1. Is a hyperboloid of one sheet the graph of a function of two variables? Explain.
   
   x^2 +y^2-z^2=1 is not a function of two variables because for the input of two variable there are two outputs since plus and minus z yield the same thing.
   
   - Luke Levy-Moore
   
   
2. How can you identify the local extrema of f(x,y) from its contour plot?
   
   Look for concentric circles!
   
   - T.R.
   
   

For Wednesday February 25

1. What is the point of Example 2.5?
   
   The point is to be able to prove if the limit exists and if it does what it is. Therefore, we try different equations that should give the same result for the limit. In this example, x=y, x=0, y=o works, and gives us 0 as the limit. However, x=y^2 gives us 1/2 as the limit. So, we understand the limit doesn't exist as the curves get closer to the origin.
   
   - Erden Oktay
   
   
2. Why do you think we are studying limits now?
   
   I think we are now studying limits because we will be taking derivatives and integrals of multi variable functions, and limits are the foundation of those two calculations.
   
   - Megan Geen
   

For Friday February 27

1. For f(x,y), what information does f_x(1,0) give?
   
   f_x(1,0) is the partial derivative of f with respect to x which gives the instantaneous rate of change in the x direction at the point (1,0).
   
   - Becky Johnson
   
   
2. How many second-order partial derivatives does g(x,y,z) have?
   
   There are nine second-order partial derivatives for g(x,y,z). Taking a first derivative gives 3 equations; one with respect to x, another with respect to y, and the last with respect to z.
   
   To find the second order derivative for g(x,y,z), we must derive all three of first-order derivatives. If we complete the same process as before, each of the three first-order derivatives will produce three second-order derivatives, making a total of 9.
   
   - Aidan Kestigian
   

For Wednesday March 4

1. If f(x,y) is a well-behaved function and has a local maximum at (a,b), what can you say about the linear approximation to f(x,y) at (a,b)?
   
   If the function has a local maximum at (a,b) the linear approxiamtion will be the tangent in the z direction, so it will be the plane tangent to the maximum, and parallel to the xy plane.
   
   - Julia Simundza
   
   
2. Let L(x,y) be the linear approximation of f(x,y) at (a,b). What graphical properties of the surface z=f(x,y) would make L(x,y) particularly accurate? particularly inaccurate?
   
   If the surface is reasonably flat at the point (a,b), the Linear Approximation at the point (a,b) will be more accurate than if the surface is especially curved. Any sharp points would make the Linear Approximation less accurate.
   
   In general, if the surface is well behaved at the point (a,b) and has minimal sporadic curving, the Linear Approximation of the surface at (a,b) will be more accurate.
   
   - Molly Thunberg
   

For Monday March 16

Suppose that w=f(x,y,z) and that x,y,z are all function of r,s,t. How many partial derivatives do you need to calculate in order to determine dw/dt?


6 partial derivatives need to calculate in order to determine the dw/dt.

They are dw/dx, dw/dy, dw/dz,dx/dt,dy/dt and dz/dt.

- Alfred Zhou

For Friday March 20

1. Explain the idea of a directional derivative your own words.
   
   A directional derivative describes the rate of change of a function, in a particular direction. It is not simply along the x or y axis as we have been doing up until now, it takes both x and y components into consideration, a more "complex" direction.
   
   - Ali Melhorn
   
   
2. What type of quantity is gradient of a function f(x,y)?
   
   The gradient of a function f(x,y) is a vector-valued function.
   
   - Jen Shields
   
   
3. What information does the gradient give you about f(x,y)?
   
   The gradient provides us with the direction of the greatest rate of increase in the function and the magnitude of the greatest rate of change in the function.
   
   - Russ Forman
   

For Monday March 23

1. If the partials f_x and f_y exist everywhere, at what points (x₀, y₀) can f have a local max or a local min?
   
   If the partial derivatives exist everywhere, the local maximum and minimum only exist when the partial derivatives = 0 or do not exist
   
   - Jeff Kleinschmidt
   
   
2. Suppose that f is a well-behaved function where f_x(3,4)=0, f_y(3,4)=0, f_xx(3,4)=2, f_yy(3,4)=-3, and f_xy(3,4)=-2. Will (3,4) be a local max, min, or neither of f? Why?
   
   (3,4) is not a max or a min of f because the discriminant of f(3,4)=-10, and for a point to be an extrema of f, the discriminant must be greater than zero.
   
   - Laura Richardson
   
   
3. Explain the idea behind the method of steepest ascent in your own words.
   
   To find the steepest ascent:
   • You move from the initial guess of the max or min in the direction of the gradient.
   • Keep moving in this same direction until the function stops increasing.
   • Then from this point, find a new gradient and move in this direction until the function stops increasing.
   • Continue moving in this way until the two points where we changed direction are close together.
     
     
   - Stephanie Jones

For Friday March 27

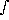
1. If f(x,y) is a function of two variables, what does 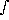_R f(x,y) dA measure?
   The double integral tells us the volume of the figure bounded by the surface of your function, the xy plane, and the bounds of x and y.
   
   - Jon Lecznar
   
   
2. Explain Fubini's Theorem in your own words. What is its importance?
   
   Fubini's Theorem breaks double integrals into two iterated integrals. This says that the double integral can be written in two ways, choosing either of the iterated integrals to start the notation, and it will mean the same double integral.
   
   - Julia Simundza
   

For Wednesday April 1

1. What do the coordinates (r,theta) in polar coordinates measure?
   
   it measures a point that is "r" distance away from the origin and if you were to draw a line from the point to the origin, there would be a angle of theta in between the line and the (positive) x-axis
   
   - Rebecca Tate
   
   
2. Why does finding area by integration in polar coordinates differ from finding area by integration in rectangular coordinates?
   

Integration with polar coordinates consists of adding up all the circular sectors within a given function. In other words, theta is broken up into infinitesimal thetas.

The area of a circular sector is 1/2 (r^2)(theta), so integrating over all infinitesimal thetas gives the expression A= [integral] 1/2 (r^2)(d-theta).

- Vanessa D'Amico

For Friday April 3

1. Why would you ever want to convert a double integral from rectangular to polar coordinates?
   
   The reason of we want to convert a double integral from rectangular to polar coordinates is if the region over which we are integrating is in some way circular, polar coordinates may be exactly what we need for dealing with an otherwise intractable integration problem.
   
   - Alfred Zhou
   
   
2. What is the shape of a polar rectangle?
   
   The rectangle for polar coordinates is a elementary polar regions it is bounded by 2 circular arcs and two rays.
   
   - Eastern Hsu
   

For Wednesday April 8

1. Give a real-world example where you would want to compute surface area.
   
   In biology, surface area of a tissue is important for maximum absorption of water or nutrients. For example, the small intenstines have a bumpy, textured surface in order to increase the surface area and thus increase the space available for absorption. This biological system could serve as a model, and the parameters of the curves of these bumps could be calculated if someone wanted to apply this to enhancing absorbtion by a synthetic material.
   
   - Julia Simundza
   
   
2. After partitioning the region R, what object is used to approximate the surface area over each subregion R_i?
   
   We use little parallelograms tangent to subregions Ri in order to approximate the surface area.
   
   - Erden Oktay
   

For Friday April 10

1. Explain why Graph B in Example 1.3 is not the actual graph of a vector field but is just a representation of the graph of a vector field.
   
   Graph B in Example 1.3 is not the actual graph of a vector field but is just a representation of the graph of a vector field because the a true graph of a two-dimensional vector field would be four-dimensional, which cannot be drawn, but through the representation we can visualize many of the important properties by plotting a number of values of the vector field.
   
   - Jen Shields
   
   
2. If a particle is dropped onto Figure 14.7a at the point (-1,1), describe the path the particle will follow.
   
   It will first travel right bearing a little north, then as it goes further right it will begin to break upward more and more drastically until eventually it is traveling almost vertically.
   
   - Jon Lecznar
   

For Wednesday April 15

Give two different uses for the line integral.

The line integral can be used to calculate the mass of something traced by a curve, such as a spring. It can also be used to compute the work a force field can exert on an object moving on a certain course.

- Aidan Kestigan

For Monday April 20

1. Why are conservative vector fields your friend when evaluating line integrals?
   
   It is our friend because we don't need to parameterize the path to compute a line integral.
   
   - Eastern Hsu
   
   
2. Why is Theorem 3.2 call the Fundamental Theorem for line integrals?
   
   Theorem 3.2 is called the Fundamental Theorem for line integrals because it is comparable to the Fundamental Theorem of Calculus.
   
   The Fundamental Theorem for line integrals is f(x2,y2)-f(x1,y1), which corresponds to the Fundamental Theorem of Calculus which is F(b)-F(a). Both theorems share the same principles.
   
   - Jen Shields
   

For Friday April 24

1. What surprises you about Green's Theorem?
   
   Green's Theorem surprises me because a single line integral of a curve defined by the functions M and N is equal to the double integral of a region defined by the partial derivatives of M and N.
   
   It seems strange that a single integral of a function would be equal to the double integral of the DERIVATIVES associated with that function.
   
   - Vanessa D'Amico
   
   
2. Give an example of a region R in the plane where Green's Theorem does not hold.
   
   Greens theorem does not hold in a region R where R is defined by a curve that is not closed.
   
   - Russell Forman