Math 236 Multivariable Calculus, Reading Assignments

I'll use Maple syntax for mathematical notation on this page. All numbers indicate sections from Multivariable Calculus, Second Edition by Smith/Minton.

For Friday January 28

To read : All

1. Is (a.b).c the same as a.(b.c)?
2. In what direction does proj_ba point?
3. When is comp_ba equal to comp_ab?

For Monday January 31

To read : All

1. How is axb related to a and b geometrically?
2. Why don't we define axb for vectors in the plane?

For Wednesday February 2

To read : All

1. What information about a line L do you need to determine an equation for the line?
2. What information about a plane P do you need to determine an equation for the plane?

For Friday February 4

To read : All

1. What does the trace in the xy-plane look like?
2. What do the traces in the planes y=k look like?

For Monday February 7

To read : All

1. Consider the graph of the vector-valued function r(t)=cos(t)i - sin(t)j. Is this the graph of a function y=f(x)? Explain.
2. What are some advantages to using vector-valued functions?

For Wednesday February 9

To read : All

1. If r(t) is a vector-valued function, what geometric information does r'(t) give you?
2. If the graphs of r(t) and s(t) are the same, will r'(0) be the same as s'(0)? Explain.

For Friday February 11

To read : All. Be sure to understand Examples 3.4 and 3.5.

1. What quantity does the magnitude of the velocity vector give?
2. How would including air resistance in Example 3.4 complicate issues?

For Monday February 14

For Wednesday February 16

To read : All

1. Explain the idea of curvature in your own words.
2. If the helix in Example 4.5 were changed to r(t)=< 2sin(t), 2cos(t), 4t²>, will the curvature still be constant? Don't actually do the calculation, but give an intuitive justification.

For Friday February 18

To read : Through the section Tangential and Normal Components of Acceleration.

1. Suppose you are skiing down a hill that curves left. Describe the directions of the unit tangent, principle unit normal, and binormal vectors.
2. Why do you want the normal component of acceleration to be small when steering a car through a curve?

For Monday February 21

Finish reading the section, but no Reading Questions for today.

For Wednesday February 23

To read : All

1. Is a hyperboloid of one sheet the graph of a function of two variables? Explain.
2. How can you identify the local extrema of f(x,y) from its contour plot?

For Friday February 25

To read : All

1. What is the point of Example 2.5?
2. Why do you think we are studying limits now?

For Monday February 28

For Wednesday March 2

To read : All

1. For f(x,y), what information does f_x(1,0) give?
2. How many second-order partial derivatives does g(x,y,z) have?

For Friday March 4

For Monday March 7

To read : All

1. If f(x,y) is a well-behaved function and has a local maximum at (a,b), what can you say about the linear approximation to f(x,y) at (a,b)?
2. Let L(x,y) be the linear approximation of f(x,y) at (a,b). What graphical properties of the surface z=f(x,y) would make L(x,y) particularly accurate? particularly inaccurate?

For Wednesday March 9

To read : All

Suppose that z=f(x,y,z) and that x,y,z are all function of r,s,t. How many partial derivatives do you need to calculate in order to determine dz/dt?

For Friday March 11

For March 14 - 18

For Monday March 21

For Wednesday March 23

To read : All

1. Explain the idea of a directional derivative your own words.
2. What type of quantity is gradient of a function f(x,y)?
3. What information does the gradient give you about f(x,y)?

For Friday March 25

To read : All

1. If the partials f_x and f_y exist everywhere, at what points (x₀, y₀) can f have a local max or a local min?
2. Suppose that f is a well-behaved function where f_x(3,4)=0, f_y(3,4)=0, f_xx(3,4)=2, f_yy(3,4)=-3, and f_xy(3,4)=-2. Will (3,4) be a local max, min, or neither of f? Why?
3. Explain the idea behind the method of steepest ascent in your own words.

For Monday March 28

For Wednesday March 30

For Friday April 1

To read : All

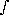
1. If f(x,y) is a function of two variables, what does 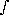_R f(x,y) dA measure?
2. Explain Fubini's Theorem in your own words. What is its importance?

For Monday April 4

For Wednesday April 6

To read : All

Why is M_y, the moment about the y-axis, used to compute the x-coordinate of the center of mass?

For Friday April 8

To read : All

1. Why would you ever want to convert a double integral from rectangular to polar coordinates?
2. What is the shape of a polar rectangle?

For Monday April 11

To read : All

1. Give a real-world example where you would want to compute surface area.
2. After partitioning the region R, what object is used to approximate the surface area over each subregion R_i?

For Wednesday April 13

To read : All

1. Explain why Graph B in Example 1.3 is not the actual graph of a vector field but is just a representation of the graph of a vector field.
2. If a particle is dropped onto Figure 14.7a at the point (-1,1), describe the path the particle will follow.

For Friday April 15

To read : All

Give two different uses for the line integral.

For Monday April 18

For Wednesday April 20

For Friday April 22

To read : All

1. Why are conservative vector fields your friend when evaluating line integrals?
2. Why is Theorem 3.2 call the Fundamental Theorem for line integrals?

For Monday April 25

To read : All

1. What surprises you about Green's Theorem?
2. Give an example of a region R in the plane where Green's Theorem does not hold.

For Wednesday April 27

For Friday April 29

To read : All

1. Why would you want to compute a triple integral?
2. What is often the hardest part of calculating a triple integral?

For Monday May 2

To read : All

1. What are some of the advantages to using cylindrical coordinates?
2. What disadvantages are there?