Math 236 - Multivariable Calculus
Reading Assignments - November & December 2001

Be sure to check back, because this may change during the semester.
(Last modified: Friday, November 2, 2001, 1:40 PM )

I'll use Maple syntax for mathematical notation on this page.
All numbers indicate sections from Multivariable Calculus by Ostebee/Zorn.

For November 2

No reading assignment. Work on Project 2.

For November 5

Section 2.8 The Chain Rule
  • To read : All
  • Be sure to understand : The definition of the derivative matrix, the statement of the Chain Rule (Theorem 4), and Example 5.

Email Subject Line : Math 236 11/5 Your Name

Reading Questions:

  1. If f:R5 -> R3, how many rows does the derivative matrix of f contain? How many columns?
  2. If f:R3 -> R4 and g:R4 -> R5, what will the dimensions of the derivative matrix of g o f be?

For November 7

Section 3.1 Multiple Integrals and Approximating Sums
  • To read : All
  • Be sure to understand : The section Approximating Sums on page 173 and the definition of the double integral as a limit on page 175

Email Subject Line : Math 236 11/7 Your Name

Reading Question:

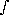
  1. If f(x,y) is a function of two variables, what does 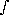R f(x,y) dA measure?
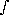
  2. For any region R in the plane, what does 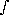R 1 dA measure?

For November 9

Section 3.2 Calculating Integrals by Iteration
  • To read : All
  • Be sure to understand : The section "Iteration: why it works"

Email Subject Line : Math 236 11/9 Your Name

Reading Question:

    What is the advantage of calculating double integrals by iteration?

For November 12

Section 3.2 Calculating Integrals by Iteration
Reread the section, especially the proof of Theorem 1 but there are no reading questions for today.

For November 14

Inclass part of Exam 2 today. No Reading Assignment.

For November 16

Appendix B Calculus in Polar Coordinates
  • To read : All, but you can de-emphasize the part before the section on Finding Area in Polar Coordinates
  • Be sure to understand : The section Finding Area in Polar Coordinates

Email Subject Line : Math 236 11/16 Your Name

Reading Question :

    When approximating an area in rectangular coordinates, we form rectangles each of width x. In polar coordinates, what do we form rather than rectangles?

For November 19

Section 3.3 Double Integrals in Polar Coordinates
  • To read : All
  • Be sure to understand : The section "Polar Integration - How It Works"

Email Subject Line : Math 236 11/9 Your Name

Reading Questions :

  1. Why would you ever want to convert a double integral from rectangular to polar coordinates?
  2. What is the shape of a polar rectangle?

For November 26

Section 5.1 Line Integrals
  • To read : All
  • Be sure to understand : The definitions of a vector field and of the line integral

Reading Questions :
Since this is the first day after break, you don't have to send these in, but you should think about them.

  1. Consider the vector field graphed in Example 2. If you dropped a particle at the point (-2,4), describe the path that the particle would follow.
  2. Consider the vector field graphed in Example 1. If you dropped a particle at the point (2,2), describe the path the particle would follow.

For November 28

Section 5.1 Line Integrals
  • To read : Reread the section for today.

Email Subject Line : Math 236 11/28 Your Name

Reading Question :

    What is a physical interpretation of the line integral? Does this make sense to you?

For November 30

Section 5.2 More on Line Integrals; A Fundamental Theorem
  • To read : All
  • Be sure to understand : The statements of Theorem 1 and 2, and Example 4.

Email Subject Line : Math 236 11/30 Your Name

Reading Question :

    Let g1 be the parametrization g1(t)=(t, 2t) for 0<=T<=2 and g2 be the parametrization g2(t)=(2t, 4t) for 0<=T<=1.
    How are g1f(X) dX and g2f(X) dX related?

For December 3

Section 5.2 More on Line Integrals; a Fundamental Theorem
  • To read : All
  • Be sure to understand : The statement of Theorem 2

Email Subject Line : Math 236 12/2 Your Name

Reading Questions:

  1. What is a potential function ?
  2. What is the advantage of potential functions when calculating line integrals?

For December 5

Section 5.3 Relating Line and Area Integrals: Green's Theorem
  • To read : Through page 271
  • Be sure to understand : The statement of Green's Theorem. This is a hard section. We'll talk about the proof in class.

Email Subject Line : Math 236 12/5 Your Name

Reading Questions:

  1. What are the two types of functions involved in Green's Theorem? Is this surprising?
  2. In non-technical terms, what is special about the curve in Green's Theorem?

For December 7

Section 5.3 Relating Line and Area Integrals: Green's Theorem
  • To read : Reread through page 271
  • Be sure to understand : All the conditions of Green's Theorem

Email Subject Line : Math 236 12/7 Your Name

Reading Question:

    Give an example of a region R in the plane where Green's Theorem does not apply.
Math 236 Home | T. Ratliff's Home
Maintained by Tommy Ratliff, tratliff@wheatonma.edu
Last modified: Friday, November 2, 2001, 1:40 PM