Math 221 - Linear Algebra - Reading Assignments
September 1999

Be sure to check back, because this may change during the semester.
Last modified: Wednesday, August 18, 1999, 1:44 PM

I'll use Maple syntax for mathematical notation on this page.
All numbers indicate sections from Linear Algebra and Its Applications by David Lay.

For September 14

Introduction to Chapter 1
Section 1.1 Systems of Linear Equations
Section 1.2 Row Reduction and Echelon Forms
  • To read : All
  • Be sure to understand : Example 2 in 1.1, the section "Existence and Uniqueness Questions" in 1.2

Email Subject Line : Math 221 9/14 Your Name

Reading Questions :

    Let A be the matrix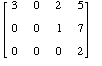
  1. Is A is row echelon form? Why or why not?
  2. What values are in the pivot positions of A?
  3. Suppose that A is the augmented matrix for a system of 3 equations in 3 unknowns. Is the system consistent or inconsistent? Explain.

For September 16

Section 1.3 Vector Equations
  • To read : All
  • Be sure to understand : The section "Linear Combinations" and the definition of Span{u,v}

Email Subject Line : Math 221 9/16 Your Name

Reading Questions :

  1. Let y=(1,2,3), u=(1,0,0) and v=(0,4,6). Write y as a linear combination of u and v.
  2. Let u=(1,0,0) and v=(0,1,0). Give a geometric description of Span{u, v}.

For September 21

Section 1.4 The Matrix Equation Ax=b
Section 1.5 Solution Sets of Linear Systems
  • To read : All
  • Be sure to understand : The statement of Theorem 4 in 1.4, Example 3 and the statement of Theorem 6 in 1.5

Email Subject Line : Math 221 9/21 Your Name

Reading Questions :

  1. Suppose A is a 4x5 matrix with 3 pivots. Do the columns of A span R4?
  2. Explain the difference between a homogeneous system of equations and a non-homogeneous system of equations.
  3. If the system Ax=b is consistent and Ax=0 has a non-trivial solution, how many solutions does Ax=b have?

For September 23

Section 1.6 Linear Independence
  • To read : All
  • Be sure to understand : The section "Linear Independence of Matrix Columns"

Email Subject Line : Math 221 9/23 Your Name

Reading Questions :

  1. If Ax=0 has infinitely many solutions, can the columns of A be linearly independent? Explain.
  2. If Ax=b has infinitely many solutions, can the columns of A be linearly independent? Explain.
  3. Explain in your own words why a set of three vectors in R2 cannot be linearly independent.

For September 28

Section 1.7 Introduction to Linear Transformations
  • To read : All
  • Be sure to understand : Example 1, the definition of a linear transformation

Email Subject Line : Math 221 9/28 Your Name

Reading Questions :

  1. Let T:R2 -> R2 be a transformation defined by T(x1, x2) = (x1+2, x2 + 3). Is T a linear transformation? (Hint: Look at Property 3)
  2. If T:R5 -> R3 is a linear transformation where Tx=Ax, what is the size of the matrix A?

For September 30

Section 1.8 The Matrix of a Linear Transformation
  • To read : All
  • Be sure to understand : Examples 1 and 2, the definition of one-one and onto, the statement of Theorems 11 and 12

Email Subject Line : Math 221 9/30 Your Name

Reading Questions :

  1. Give the matrix A for the linear transformation T:R2 -> R2 that expands horizontally by a factor of 2.
  2. Let T:R5 -> R3 be a linear transformation with standard matrix A where A has three pivots. Is T one-one? Explain.


Math 221 Home | T. Ratliff's Home

Maintained by Tommy Ratliff, tratliff@wheatonma.edu
Last modified: Wednesday, August 18, 1999, 1:44 PM