Math 221 - Linear Algebra - Reading Assignments
October 1999

Be sure to check back, since these may change.
Last modified: Thursday, August 19, 1999, 12:51 PM

I'll use Maple syntax for mathematical notation on this page.
All numbers indicate sections from Linear Algebra and Its Applications by David Lay.

For October 5

Introduction to Chapter 2
Section 2.1 Matrix Operations
Section 2.2 The Inverse of a Matrix
  • To read : All
  • Be sure to understand : The section "Matrix Multiplication" and Example 3 in 2.1, the statement of Theorems 5 and 7 in 2.2

Email Subject Line : Math 221 10/5 Your Name

Reading Questions :

  1. Give one way in which matrix multiplication differs from multiplication of real numbers.
  2. Suppose A is invertible. Can Ax=b have infinitely many solutions?

For October 7

Section 2.3 Characterizations of Invertible Matrices
  • To read : All
  • Be sure to understand : The statement of Theorem 8

Reading Questions : Exam 1 due today. No Reading Questions.

For October 13

Fall Break - No Reading Assignment

For October 14

Section 1.9 Linear Models in Business, Science, and Engineering
Section 4.9 Applications to Markov Chains
  • To read : The section "Difference Equations" in 1.9 and all of 4.9
  • Be sure to understand : The section "Predicting the Distant Future" in 4.9

Email Subject Line : Math 221 10/14 Your Name

Reading Questions:

  1. What is the point of studying Markov chains?
  2. What is a steady state vector for a stochastic matrix P?
  3. What is special about regular stochastic matrices?

For October 19

Section 2.8 Applications to Computer Graphics
  • To read : Thru the section "Homogeneous 3D Coordinates"
  • Be sure to understand : Examples 4, 5, and 6.

Email Subject Line : Math 221 10/19 Your Name

Reading Question:

    What is the advantage of using homogeneous coordinates in computer graphics?

For October 21

Introduction to Chapter 3
Section 3.1 Introduction to Determinants
Section 3.2 Properties of Determinants
  • To read : All
  • Be sure to understand : The definition of the determinant, and the statements of Theorems 3, 4, and 6

Email Subject Line : Math 221 10/21 Your Name

Reading Questions :

  1. Why do we care about finding det(A)?
  2. If A = 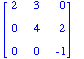, what is det(A)?

For October 26

Introduction to Chapter 4
Section 4.1 Vector Spaces and Subspaces
Section 4.2 Null Spaces, Column Spaces, and Linear Transformations
  • To read : All, but you can skip Examples 2, 3, and 5 in 4.1
  • Be sure to understand : The definition of a vector space, Examples 4 and 8 in Section 4.1, the definition of a subspace, the statement of Theorem 1, and the section "The Contrast Between Nul A and Col A" in Section 4.2

Email Subject Line : Math 221 10/26 Your Name

Reading Questions :

  1. Give an example of a subset of R2 that is not a subspace of R2.
  2. True or false: If A is a 3 x 5 matrix, then the nullspace and column space of A are subspaces of R3.

For October 28

Section 4.3 Linearly Independent Sets; Bases
  • To read : All
  • Be sure to understand : Definition of a basis, Theorem 5, and the section "Two Views of a Basis"

Email Subject Line : Math 221 10/28 Your Name

Reading Questions :

  1. Let v1=(1,2), v2=(3,4), and v3=(4,6). Give a basis for H=Span{v1, v2, v3}.
  2. If A is a 4 x 5 matrix with three pivot positions, how many vectors does a basis for Col A contain?


Math 221 Home | T. Ratliff's Home

Maintained by Tommy Ratliff, tratliff@wheatonma.edu
Last modified: Thursday, August 19, 1999, 12:51 PM