Math 221 - Linear Algebra - Reading Assignments
November 1999

Be sure to check back, since these may change.
(Last modified: Wednesday, August 18, 1999, 3:32 PM )

I'll use Maple syntax for mathematical notation on this page.
All numbers indicate sections from Linear Algebra and Its Applications by David Lay.

For November 2

Reread Section 4.3, but no Reading Questions for today.

For November 4

Section 4.5 The Dimension of a Vector Space
Section 4.6 Rank
  • To read : All
  • Be sure to understand : Theorems 10, 11, and 12 in 4.5 and the definition of rank, the Rank Theorem, the continuation of the Invertible Matrix Theorem in 4.6

Email Subject Line : Math 221 11/4 Your Name

Reading Questions :

  1. What is the dimension of R3? Why? Does this make sense geometrically?
  2. Can there be a set of linearly independent vectors {v1,v2,. . ., v12} that does not span R12? Explain.
  3. If A is 4x7 with three pivots, what is the dimension of Nul A? Why?

For November 9

Section 5.1 Eigenvectors and Eigenvalues
  • To read : All
  • Be sure to understand : The definitions of eigenvector and eigenvalue, and Examples 3 and 4

Email Subject Line : Math 221 11/9 Your Name

Reading Questions:

  1. Let A=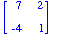. Verify that (1,-2) is an eigevector of A with corresponding eigenvalue 3.
  2. Suppose A is 3x3 with eigenvalues 1, 2, and 5. What is the dimension of nul(A)?

For November 11

Section 5.2 The Characteristic Equation
  • To read : All, but the section on Determinants should be review
  • Be sure to understand : The definition of the characteristic equation, Example 3, and the definition of similarity

Email Subject Line : Math 221 11/11 Your Name

Reading Questions:

  1. Let A=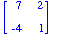. Find the characteristic equation of A.
  2. How is the characteristic equation of a matrix related to the eigenvalues of the matrix?

For November 16

Section 5.3 Diagonalization
  • To read : All
  • Be sure to understand : Example 3

Email Subject Line : Math 221 11/16 Your Name

Reading Questions:

  1. What is the point of finding a diagonalization of a matrix?
  2. If A is 4x4 with eigenvalues 1, 2, 0, 3, is A diagonalizable? Explain.

For November 18

Section 5.6 Discrete Dynamical Systems
  • To read : Through Example 4
  • Be sure to understand : Example 1 and the plots in Examples 2, 3, and 4

Exam 2 due today. No Reading Questions.

For November 23

Section 6.1 Inner Product, Length, and Orthogonality
  • To read : All
  • Be sure to understand : The definitions of the inner product, norm, and orthogonal complement

Email Subject Line : Math 221 11/23 Your Name

Reading Questions :

  1. Are the two vectors u=(3,1) and v=(-2,3) in R2 orthogonal? Why or why not?
  2. Let W be the xz-plane in R3. What is the orthogonal complement of W?

For November 25

Thanksgiving Break.

For November 30

Section 6.2 Orthogonal Sets
  • To read : Through the section "Decomposing a Force into Component Forces"
  • Be sure to understand : The statement of Theorem 4 and Figure 4

Email Subject Line : Math 221 11/30 Your Name

Reading Questions :

  1. Give an example of an orthogonal basis for R3.
  2. Let w be the orthogonal projection of y onto u. What direction does w point? What direction does y - w point?


Math 221 Home | T. Ratliff's Home

Maintained by Tommy Ratliff, tratliff@wheatonma.edu
Last modified: Wednesday, August 18, 1999, 3:32 PM