
|
Math 236 - Multivariable Calculus - Reading Assignments
October 1998
|
Be sure to check back, because this may change during the semester.
(Last modified:
Friday, October 23, 1998,
10:42 AM )
I'll use Maple syntax for mathematical notation on this page.
All numbers indicate sections from Multivariable Calculus by Ostebee/Zorn.
 For October 2 For October 2
Section 2.1 Functions of several variables
No Reading Questions for today
 For October 5 For October 5
Section 2.2 Partial Derivatives
- To read : All
- Be sure to understand : Example 2, the formal definition of partial derivatives
Email Subject Line : Math 236 10/5 Your Name
Reading Questions : Let f(x,y)=x2y + 3xy - y.
- Find fx(x,y) and fy(x,y).
- Is f increasing or decreasing in the x direction at the point (2,1)? Why?
 For October 7 For October 7
Section 2.2 Partial derivatives (continued)
- To read : Reread the section
- Be sure to understand : Examples 4 & 5, the statement of Theorem 1
Email Subject Line : Math 236 10/7 Your Name
Reading Question :
Find all stationary points of f(x,y)=x2 +2xy+y2
 For October 9 For October 9
Section 2.3 Partial derivatives and linear approximations
- To read : All
- Be sure to understand : The section "Partial derivatives, the cross product,
and the tangent plane" and the defintion of linear approximation
Email Subject Line : Math 236 10/9 Your Name
Reading Question :
Find the linear approximation to f(x,y)=x2y +3xy-y2
at the point (2,1).
 For October 14 For October 14
Section The gradient and directional derivatives
- To read : All
- Be sure to understand : The definition of the gradient
No reading questions since this is the first day after break.
 For October 16 For October 16
Section 2.4 The gradient and directional derivatives (continued)
- To read : Reread the section
- Be sure to understand : The section "Gradient vectors and linear approximation"
Email Subject Line : Math 236 10/16 Your Name
Reading Questions :
- What information does the directional derivative give you?
- For a function f(x,y), how many components does the gradient
vector contain?
 For October 19 For October 19
Section 2.5 Local Linearity: theory of the derivative
- To read : All
- Be sure to understand : Example 1, the definition of the total derivative
Email Subject Line : Math 236 10/19 Your Name
Reading Question:
What is the point of Example 1?
 For October 21 For October 21
Section 2.6 Higher Order Derivatives and Quadratic Approximations
- To read : All
- Be sure to understand : The statement of Theorem 2, and the section
"Taylor polynomials in several variables"
Email Subject Line : Math 236 10/21 Your Name
Reading Questions:
- If f(x,y)=x3y2+2xy, what is fxy?
- Is there a function f(x,y) where fxy=2xy+y and
fyx=x2y+x? Explain.
 For October 23 For October 23
Work on Project 2 - No reading assignment.
 For October 26 For October 26
Section 2.8 The Chain Rule
- To read : All
- Be sure to understand : The definition of the derivative matrix, the statement of the Chain Rule (Theorem 4), and Example 5. You can de-emphasize pp
164, 165, and 166 (up to the Chain Rule) - We'll talk about this in more depth on Wednesday.
Email Subject Line : Math 236 10/26 Your Name
Reading Questions:
- If f:R5 -> R3, how many rows does the derivative matrix of
f contain? How many columns?
- If f:R3 -> R4 and g:R4 -> R5, what will the dimensions of the derivative matrix of g o f be?
 For October 28 For October 28
Section 2.8 The Chain Rule (continued)
- To read : Re-read the section
- Be sure to understand : The section "Derivatives and linear functions" on pg 161 and Example 2
Email Subject Line : Math 236 10/28 Your Name
Reading Question:
Explain why the chain rule for functions of one variable should work.
(You can paraphrase the book, but don't just quote it.)
 For October 30 For October 30
Section 3.1 Multiple Integrals and Approximating Sums
- To read : All
- Be sure to understand : The section Approximating Sums on page 173 and the definition of the double integral as a limit on page 175
Email Subject Line : Math 236 10/30 Your Name
Reading Question:
- If f(x,y) is a function of two variables, what does
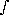 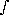 R f(x,y) dA measure? R f(x,y) dA measure?
- For any region R in the plane, what does
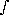 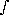 R 1 dA measure? R 1 dA measure?
Math 236 Home |
T. Ratliff's Home
|