Math 221 - Linear Algebra - Reading Assignments
September 1998

Be sure to check back, because this may change during the semester.
(Last modified: Wednesday, August 26, 1998, 11:04 AM )

I'll use Maple syntax for mathematical notation on this page.
All numbers indicate sections from Linear Algebra and Its Applications by David Lay.

For September 8

Introduction to Chapter 1
Section 1.1 Systems of Linear Equations
Section 1.2 Row Reduction and Echelon Forms
Section 1.3 Vector Equations
  • To read : All
  • Be sure to understand : Example 2 in 1.1, the section "Existence and Uniqueness Questions" in 1.2, the section "Linear Combinations" in 1.3

Email Subject Line : Math 221 9/8 Your Name

Reading Questions :

  1. Let A be the matrix
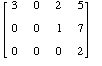
    • Is A is row echelon form? Why or why not?
    • What values are in the pivot positions of A?
  2. Let u=(1,0,0) and v=(0,1,0). Give a geometric description of Span{u, v}.

For September 10

Section 1.4 The Matrix Equation Ax=b
Section 1.5 Solution Sets of Linear Systems
  • To read : All
  • Be sure to understand : The statement of Theorem 4 in 1.4, Example 3 and the statement of Theorem 6 in 1.5

Email Subject Line : Math 221 9/10 Your Name

Reading Questions :

  1. Suppose A is a 4x5 matrix with 3 pivots. Do the columns of A span R4?
  2. Explain the difference between a homogeneous system of equations and a non-homogeneous system of equations.
  3. If the system Ax=b is consistent and Ax=0 has a solution, how many solutions does Ax=b have?

For September 15

Section 1.6 Linear Independence
  • To read : All
  • Be sure to understand : The section "Linear Independence of Matrix Columns"

Email Subject Line : Math 221 9/15 Your Name

Reading Questions :

  1. If Ax=0 has infinitely many solutions, can the columns of A be linearly independent? Explain.
  2. If Ax=b has infinitely many solutions, can the columns of A be linearly independent? Explain.
  3. Explain in your own words why a set of three vectors in R2 cannot be linearly independent.

For September 17

Section 1.7 Introduction to Linear Transformations
  • To read : All
  • Be sure to understand : Example 1, the definition of a linear transformation

Email Subject Line : Math 221 9/17 Your Name

Reading Questions :

  1. Let T:R2 -> R2 be a transformation defined by T(x1, x2) = (x1+2, x2 + 3). Is T a linear transformation? (Hint: Look at Property 3)
  2. If T:R5 -> R3 is a linear transformation where Tx=Ax, what is the size of the matrix A?

For September 22

Section 1.8 The Matrix of a Linear Transformation
  • To read : All
  • Be sure to understand : The definition of one-one and onto, the statement of Theorems 11 and 12

Email Subject Line : Math 221 9/22 Your Name

Reading Questions :

  1. Give the matrix A for the linear transformation T:R2 -> R2 that expands horizontally by a factor of 2.
  2. Let T:R5 -> R3 be a linear transformation with standard matrix A where A has three pivots. Is T one-one? Explain.

For September 24

Section 1.9 Linear Models in Business, Science and Engineering
Introduction to Chapter 2
Section 2.1 Matrix Operations
Section 2.2 The Inverse of a Matrix
  • To read : Only read the section "Difference Equations" in 1.9, but read all of the Introduction and Sections 2.1 and 2.2
  • Be sure to understand : The section "Matrix Multiplication" in 2.1, the statement of Theorem 2.5 in 2.2

Email Subject Line : Math 221 9/24 Your Name

Reading Questions :

  1. Give one way in which matrix multiplication differs from multiplication of real numbers.
  2. Suppose A is invertible. Can Ax=b have infinitely many solutions?

For September 28

Section 2.3 Characterizations of Invertible Matrices
  • To read : All
  • Be sure to understand : The statement of Theorem 8

Reading Questions : None for today.


Math 221 Home | T. Ratliff's Home

Maintained by Tommy Ratliff, tratliff@wheatonma.edu
Last modified: Wednesday, August 26, 1998, 11:04 AM