Math 221 - Linear Algebra - Reading Assignments
October 1998

Be sure to check back, since these may change.
(Last modified: Tuesday, October 20, 1998, 2:56 PM )

I'll use Maple syntax for mathematical notation on this page.
All numbers indicate sections from Linear Algebra and Its Applications by David Lay.

For October 1

The Big Picture

No Reading Questions for today

For October 6

Section 2.8 Applications to Computer Graphics
  • To read : All
  • Be sure to understand : Examples 4, 5, and 6. We'll talk about the section "Perspective Projections" during class.

Reading Question:

    What is the advantage of using homogeneous coordinates in computer graphics?

For October 8

Section 3.1 Introduction to Determinants
Section 3.2 Properties of Determinants
  • To read : All
  • Be sure to understand : The definition of the determinant, and the statements of Theorems 3, 4, and 6

Email Subject Line : Math 221 10/8 Your Name

Reading Questions :

  1. Why do we care about finding det(A)?
  2. If A = 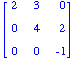, what is det(A)?

For October 13

Fall Break - No Reading Assignment

For October 15

Section 4.1 Vector Spaces and Subspaces
Section 4.2 Null Spaces, Column Spaces, and Linear Transformations
  • To read : All
  • Be sure to understand : The definition of a vector space, Examples 3 and 4 in Section 4.1, the definition of a subspace, the statement of Theorem 1, and the section "The Contrast Between Nul A and Col A" in Section 4.2

Email Subject Line : Math 221 10/15 Your Name

Reading Questions :

  1. Let Pn be the set of polynomials of degree at most n (as in Example 4 from Section 4.1). Give a subset of Pn that is not a subspace of Pn. Explain.
  2. True or false: If A is an m x n matrix, then the nullspace and column space of A are subspaces of Rm

For October 20

Section 4.3 Linearly Independent Sets; Bases
  • To read : All
  • Be sure to understand : Definition of a basis, Theorem 5, and the section "Two Views of a Basis"

Email Subject Line : Math 221 10/20 Your Name

Reading Questions :

  1. Let v1=(1,2), v2=(3,4), and v3=(4,6). Give a basis for H=Span{v1, v2, v3}.
  2. If A is 4 x 5 with three pivot positions, how many vectors does a basis for Col A contain?

For October 22

Reread Section 4.3, and resubmit the reading questions from Tuesday if you need to upgrade your answers.

For October 27

Section 4.4 Coordinate Systems
Section 4.5 The Dimension of a Vector Space
  • To read : All
  • Be sure to understand : The section "A Graphical Interpretation of Coordinates", Theorem 8, Example 7 in Section 4.4, and Theorems 10, 11, and 12 in Section 4.5

Email Subject Line : Math 221 10/27 Your Name

Reading Questions :

  1. Use the basis B from Example 4 in Section 4.4 with x=(-1,15) to find the coordinate vector [x]B relative to B.
  2. Can there be a set of linearly independent vectors {v1,v2,. . ., v12} that does not span R12? Explain.

For October 29

Section 4.6 Rank
  • To read : All
  • Be sure to understand : Definition of rank, the Rank Theorem, the continuation of the Invertible Matrix Theorem

Email Subject Line : Math 221 10/29 Your Name

Reading Questions :

  1. If A is 4x7 with three pivots, what is the dimension of Nul A? Why?
  2. If A is 5x5 with rank 3, what is det(A)? Why?


Math 221 Home | T. Ratliff's Home

Maintained by Tommy Ratliff, tratliff@wheatonma.edu
Last modified: Tuesday, October 20, 1998, 2:56 PM