Math 221 - Linear Algebra - Reading Assignments
November 1998

Be sure to check back, since these may change.
(Last modified: Thursday, November 12, 1998, 2:13 PM )

I'll use Maple syntax for mathematical notation on this page.
All numbers indicate sections from Linear Algebra and Its Applications by David Lay.

For November 3

Section 4.9 Applications to Markov Chains
  • To read : All
  • Be sure to understand : Definitions of a stochastic matrix, a Markov chain, a regular stochastic matrix, the statement of Theorem 18, and Examples 2 & 6

    Email Subject Line : Math 221 11/3 Your Name

    Reading Questions :

    1. Explain the significance of the steady state vector for a stochastic matrix.
    2. What effect does the initial state of a Markov chain have on the steady state vector?

    For November 5

    Section 5.1 Eigenvectors and Eigenvalues
    • To read : All
    • Be sure to understand : The definitions of eigenvector and eigenvalue, and Examples 3 and 4

    Email Subject Line : Math 221 11/5 Your Name

    Reading Questions:

    1. Let A=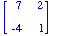. Verify that (1,-2) is an eigevector of A with corresponding eigenvalue 3.
    2. Suppose A is 3x3 with eigenvalues 1, 2, and 5. What is the dimension of nul(A)?

    For November 10

    Section 5.2 The Characteristic Equation
    • To read : All, but the section on Determinants should be review
    • Be sure to understand : The definition of the characteristic equation, Example 3, and the definition of similarity

    Email Subject Line : Math 221 11/10 Your Name

    Reading Questions:

    1. Let A=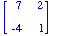. Find the characteristic equation of A.
    2. What is the point of the characteristic equation?

    For November 12

    Section 5.3 Diagonalization
    • To read : All
    • Be sure to understand : Example 3

    Email Subject Line : Math 221 11/12 Your Name

    Reading Questions:

    1. What is the point of finding a diagonalization of a matrix?
    2. If A is 4x4 with eigenvalues 1, 2, 0, 3, is A diagonalizable? Why?

    For November 17

    Section 5.4 Eigenvectors and Linear Transformations
    • To read : All, but focus on the section "Linear Transformations on Rn"
    • Be sure to understand : Figure 1 (we'll talk about this in class, too) and the statement of Theorem 8

    Reading Question:

      If A=P D P-1 then we can view A as a composite of the three transformations determined by P, D, and P-1. What does each of these three transformations do?
      (Hint: Your answer should involve the terms "change of basis" and "eigenvalue")

    For November 19

    Section 5.6 Discrete Dynamical Systems
    • To read : Through Example 5
    • Be sure to understand : Example 1 and the plots in Examples 2, 3, and 4

    Reading Questions:
    Consider the discrete dynamical system described by xk+1=Axk where A is 2x2.

    1. If the origin is an attractor, what do you know about the eigenvalues of A? (Hint: Look at example 2).
    2. If the origin is a saddle, what do you konw about the eigenvalues of A?

    For November 24

    The Big Picture
    No Reading Assignment for today.

    For November 26

    Thanksgiving Break.


    Math 221 Home | T. Ratliff's Home
    		•

    Maintained by Tommy Ratliff, tratliff@wheatonma.edu
    Last modified: Thursday, November 12, 1998, 2:13 PM