Remodeling for Monty
Montgomery Burns
Springfield
September 29, 2010
Math 104 Students
Wheaton College
Norton, MA 02766
Dear Calculus Students:
While some parts of the economy may have been experiencing less than optimal performance, the Springfield Nuclear Power Plant recorded a record profit last quarter, in no small part because so much of the regulatory attention was focussed elsewhere (thank you, BP and Massey Energy!).
To celebrate our successes, I am remodeling a portion of the bi-level atrium at the company headquarters (eligible for a tax writeoff, of course) to include a large ornamental pool with transparent polycarbonate sides and bottom that will be visible from both above at the upper level of the atrium and below at the lower level. The centerpiece of pool will be 50 floating decorative vases whose design was picked from entries submitted by the families of the employees (saving on design fees while giving the workers a false sense of influence). An insignificant child named Bert, or Bart or something similarly monosyllabic, won the contest, but that is irrelevant at this point. Now that I have the design of the vases, there are a few additional details to be worked out. When I went looking for help, your enterprising and resourceful professor naturally referred me to you.
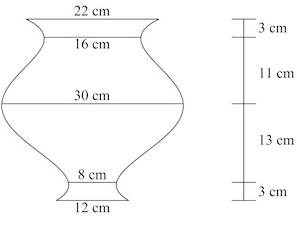
The plans call for open-top vases that are 30 cm high and are constructed of a lightweight carbon fiber that is one centimeter thick on the sides and bottom. The design requires that 15 cm of the vase is visible above water and that the remaining 15 cm below water is painted a startling metallic cerulean color to provide some visual contrast. In addition, there will be 5 thin stripes of gold ribbon on each vase running along outer surface straight down from the top rim to the flat bottom. The basic design is:
This is where I need your help. First I need to know that it is possible for the vases to float with exactly 15 cm visible above the water. If more than 15 cm is visible, then we will need to add weight into vases to make them sink to the appropriate level. The plans call for adding a special non-perishable olive oil (don't ask, I don't understand it either), and I need to know how much to add, if necessary. I also need to know the length of gold ribbons and how much cerulean paint is needed for each vase. Finally, I would like summary of the total amount of ribbon, the total amount of olive oil (if necessary), and the total amount of paint required for all 50 floating vases
In addition, the artist (I use the term very loosely) has proposed adding some smaller vases that are identical in shape, but all measurements are scaled in half so that vases are only 15 cm high and 15 cm wide at the widest point. However, due to the carbon fiber manufacturing process, each vase will still be 1 cm thick. We still want half of vase, or 7.5 cm to be visible above water. I would like your expert opinion on the viability of including these smaller vases.
After describing my needs to your enterprising and resourceful professor, he suggested that you might find it useful to know that the carbon fiber weighs approximately 1.75 grams per cubic centimeter, that the special olive oil weighs approximately 0.8 grams per cubic centimeter, and that a liter of the startling metallic cerulean paint can cover approximately 40 square meters of carbon fiber.
I realize that this is a busy time of the semester for you with your Fall Break approaching, but in order to complete the project this year and take advantage of the tax deduction, I will need your report by the end of the day on October 8.
Capitalistically yours,
Montgomery Burns
Owner, Springfield Nuclear Power Plant
A Few Comments From Your Enterprising and Resourceful Professor
The vase looks suspiciously like a surface of revolution. You will probably want to find a function to model it, and since you have five points, a fourth degree polynomial f(x)=ax4 + bx3 + cx2 + dx + k might be a good place to start.
It may also be useful to know that a floating object displaces an amount of water that is equal in weight to the weight of the object. For example, a floating object that weighs 10 kilograms will displace 10 kilograms of water. Finding the weight of the vase might be one way to proceed.
You might find it interesting that one cubic centimeter of water weighs one gram.